Square Tessellations
Twenty-five
years ago I embarked upon a university course called Vision and Structure, a
cross-curricular mathematics-art study where tessellations played a large part.
My collection of university notes has dwindled since leaving, until now I possess
only a few remaining pages, all of which come from that one unit. Perhaps they
represent the gold left after years of panning: whenever I chance across a
tiling now, I can feel a distant part of me waking up. The other day, I chanced
across the tessellation shown in Figure 1:
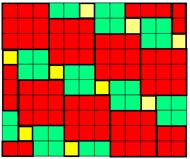
Fig. 1
This can be
seen as a tessellation of the tile in Figure 2.

Fig. 2
This tile is
built from a 1-square, a 2-square and a 3-square (throughout this article an ‘n-square’
means a square of side n units.) Thus the tessellation in Figure 1 contains
equal numbers of 1-squares, 2-squares and 3-squares. Now I knew that a tile built
from a 1-square and a 2-square can tessellate (see Figure 3) - there are many
patios up and down the land that testify to that, mine included.

Fig. 3
The question
arises, can you always find a tessellation constructed from a tile containing
equal numbers of 1-squares, 2-squares, ... up to n-squares, for any natural
number n?
Let's start by
looking at n = 4. We can certainly arrange our four tiles into what we might
call an L-shape tile, shown in Figure 4:
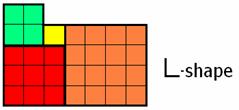
Fig. 4
This certainly
tessellates (see Figure 5):
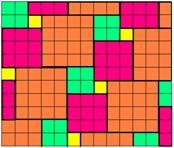
Fig. 5
Indeed, it is
easy to convince yourself that every L-shape tile will tessellate in this way. So
how far can we go with this? 1, 2, 3, 4 and 5-squares form the L-shape tile
shown in Figure 6.
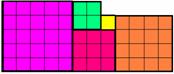
Fig. 6
However, try
as we might, we cannot form an L-shape tile from a 1-square, a 2-square… up to
a 6-square (have a go!) But we can get what we might call an S-shape tile from
these squares (see Figure 7):
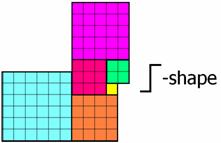
Fig. 7
Does this
tessellate? It does, forming the attractive tessellation in Figure 8.
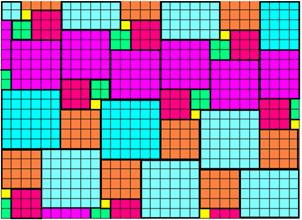
Fig. 8
We can add a 7-square
to get another S-shape (Figure 9), which also tessellates (Figure 10).
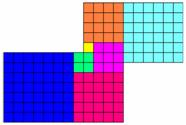
Fig. 9
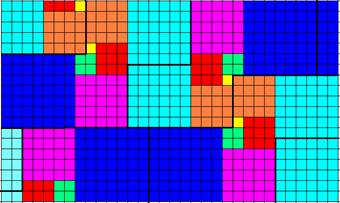
Fig. 10
We might be
forgiven for thinking that all S-shapes tessellate, but this is untrue, as experimenting
with the tile in Figure 11 shows:
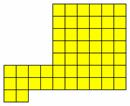
Fig. 11
At this point
we seem to come to the end of the road. However we play around with the tiles,
we can't seem to put a 1-square through to an 8-square together in a way that
will create an L-shape, or indeed a helpful S-shape. Perhaps a different tack
is needed.
Suppose that Sn
is the statement: “There exists a rectangle made up of equal numbers of
1-squares through to n-squares.” If Sn is true for all n, then as a
rectangle clearly tessellates, we will have a tile that meets our requirements.
S1
is clearly true, as is S2 (Figures 12 and 13).
![]()

Fig. 12 Fig. 13
If we now add
two 3-squares to Figure 13, we can make two rectangles that will not fit
together to make a third.
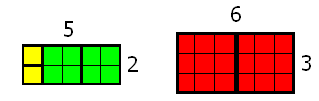
Fig. 14
However, if we
take 2×3 = 6 copies
of Figure 14, we can then build a single rectangle from the result.
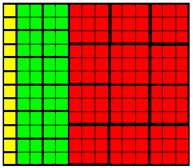
Fig. 15
So S3
is true. Can we carry out this procedure in the general case? An argument using
induction shows that we can.
Suppose Sn
is true and there is a rectangular tile (called A) containing equal numbers of
1-squares through to n-squares (suppose also there are k of each, and that A is
p by q). We can make k (n+1)-squares
into a k(n+1) by (n+1) rectangle (call this B).
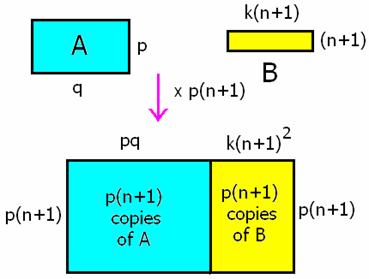
Fig. 16
Now take
(n+1)p copies of the diagram (we may not need as many as this.) We can combine
the copies of A into a (n+1)p by pq rectangle, while the copies of B will form
an (n+1)p by k(n+1)2
rectangle. These may be simply combined into a single rectangle,
containing equal numbers of 1 through to (n+1)-squares (there will be kp(n+1)
of each.)
So if Sn
is true, then Sn+1 is true, and by induction, a tile that
tessellates made from equal numbers of 1-squares through to n-squares is
possible for all n. Maybe a challenge if you happen to need a new patio?
4 April 2006, Jonny Griffiths,